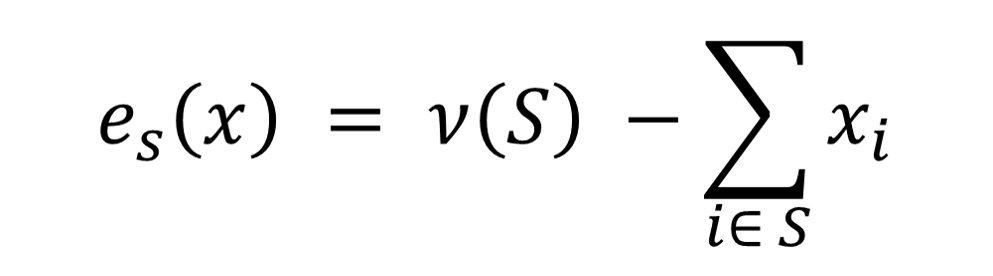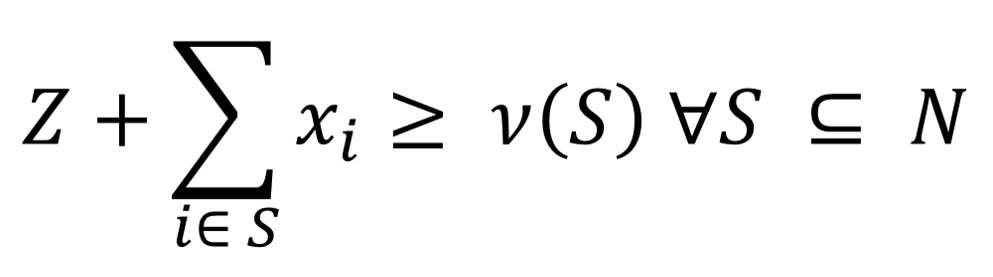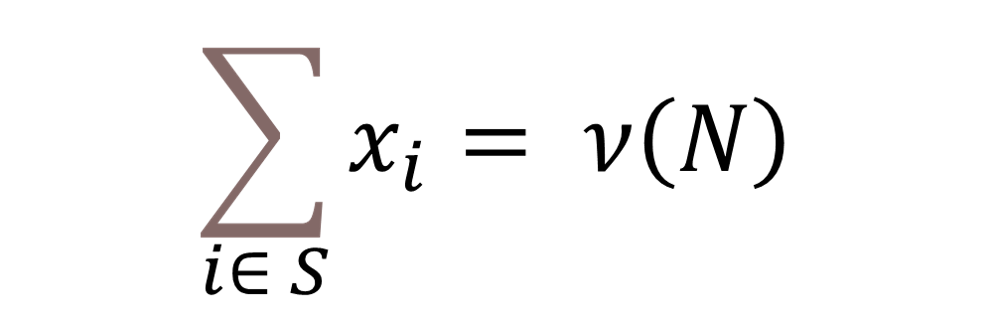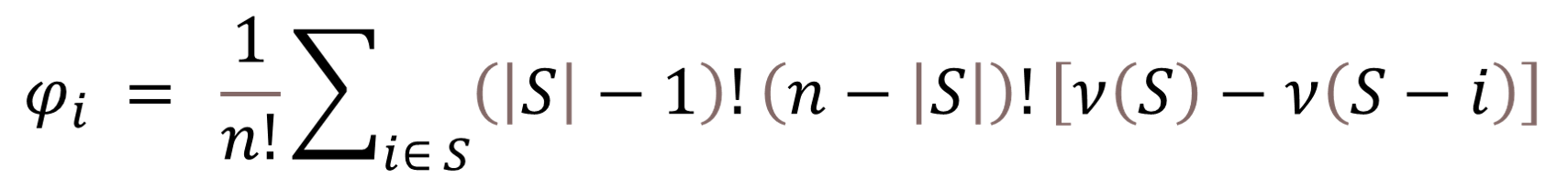Clustering is grouping set of objects based on some common characteristics. Clustering has applications in many fields, including data analysis, pattern recognition, image analysis, data compression, computer graphics, and machine learning.[1] Clustering has also been used to solve large-scale problems. Determining the number of output clusters k is challenging. In this case, using cooperative game theory provides a new way of addressing this problem by using a variety of solution concepts.[3] Cooperative Game theory (CGT) is a model of game theory where the players (also known as coalitions) use cooperative behavior in competition. It is also referred to as a coalitional game.[2] The coalition behavior of the players is monitored by external agencies under regulatory authority. [2]

Game-Theoretic Solution Concepts for the Clustering Problem

Specifying value for each coalition gives a cooperative game. The cooperative game has a finite set of players N (also known as the grand coalition) and a characteristic function ν:  2^N → R. It defines the value ν(S) of any coalition where S ⊆ N. The function describes how much collective payoff can be gained by a set of players by forming a coalition; the game is also known as value or profit game.^[1]

The formation of the grand coalition N is the main assumption in cooperative game theory. The challenge now is fairly allocating the payoff v(N) among the players. This assumption is not restrictive; even if players split off and form smaller coalitions, we apply solution concepts to the subgames defined by whatever coalitions are formed.^[4]

Let’s explore the solution concepts to utilize their properties for the clustering game. A Shapley value is based on average fairness and stability, while Nucleolus is based on both min-max fairness and stability. Of these solution concepts, Nucleolus properties are the most suitable for the clustering game.^[3] Nucleolus comes with its drawbacks, most notably that it is computationally expensive. We can use other solution concepts for computational ease. These are mentioned below:

1. 1. The Core

When the set of attainable allocations cannot be improved further by a coalition (a subset) of the economy’s agents, it is called the Core. An allocation is said to have the Core property if there is no coalition that can be improved.^[5]

Let (N, ν) be a coalitional game with transferable utility (say, TU). Let x ,…,  where is the payoff of player i. Then, the Core consists of all payoff allocations, that satisfy the following properties:

1. 1. • individual rationality, i.e., xi  ≥ ν({i}) ∀ i ∈ N
      • collective rationality i.e., ∑_{i∈ N^xi} = v(N)
      • coalitional rationality i.e., ∑_{i∈ S^xi} ≥ v(S) ∀ S ⊆ N

A payoff allocation that satisfies individual rationality and collective rationality is called an imputation.

1. 1. The Nucleolus

The allocation that minimizes the dissatisfaction of the players from the allocation they can receive in a game is the Nucleolus.^[3] For every x, consider the excess defined by

e_s(x) is a measure of the unhappiness of S with x. The goal of Nucleolus is to minimize the most unhappy coalition, i.e., the largest of the e_s(x). This could also be written in linear programming problem formulation as min Z, subject to

It combines several fairness criteria with stability. It is the central imputation, and thus in the min-max sense it is fair and optimum. If the Core is non-empty, the Nucleolus is in the Core.^[4]

1. 1. The Shapley Value

The Shapley value is the unique payoff vector that satisfies monotonicity, efficient and symmetric.^[4] To each cooperative game, it assigns a unique distribution of a total surplus generated by the coalition of all players.^[6]

If it follows the fairness-based axioms already discussed, then any imputation φ = φ₁ , …, φ_n ) is a Shapley value. For any general coalitional game with transferable utility (N, ν), the Shapley value of player i is given by

 Π = set of all permutations on N.

x_i^Π= contribution of player i to permutation π.

Clustering Based on Cooperative Game Theory

Let’s assign maximum Shapley value for each cluster as cluster center. If the center has a high density surrounding, we will consider other close points to be center; else it will consider more far away points.

In this case, an expansion queue helps to check the variation of density in a cluster. It also ensures that clusters are distinguished from each other when they are connected to a thin bridge of points.

Algorithm: DRAC (Density-Restricted Agglomerative Clustering) ^[3]

Require: Dataset, the maximum threshold for similarity δ ∈ [0, 1], and threshold for Shapley value multiplicity γ ∈ [0, 1] ^[3]

1. Start with checking pairwise similarities between all points in the dataset.
2. Compute the Shapley value for each point i.
3. Arrange the points in decreasing order of their Shapley values. Let be the global maximum of Shapley values. Start a new queue, it’ll be our expansion queue.
4. Next, start a new cluster. Of all the unallocated points, choose the point with the maximum Shapley value as the new cluster center. Let be its Shapley value. Mark those points as allocated. Add it to the expansion queue.
5. Set β = δ q
6. For each unallocated point where the similarity of that point to the first point in the expansion queue is at least β, add it to the current cluster and mark it as allocated. If the Shapley value of that point is at least γ-multiple of  l_M, add it to the expansion queue.
7. Remove the first point from the expansion queue.
8. If the expansion queue is not empty, go to step 6.
9. If the cluster center is the only point in its cluster, mark it as noise.
10. If all points are allocated a cluster, terminate.

Results

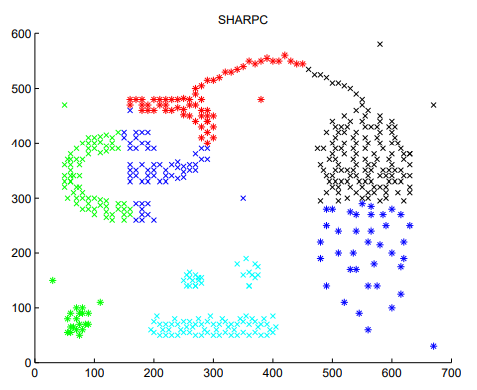
Let’s compare our algorithm with some existing algorithms. SHARPC (security- and heterogeneity-driven scheduling algorithm) proposes a novel approach to finding the cluster centers and giving a good start to K-means using a game theoretic solution concept; the Shapley value which thus results in the desired clustering. The limitation of this approach is that it is restricted to K-means; this is not always desirable, especially when the classes have unequal variances or when they lack convexity.^[3]

Fig 1: Clusters as discovered by SHARPC

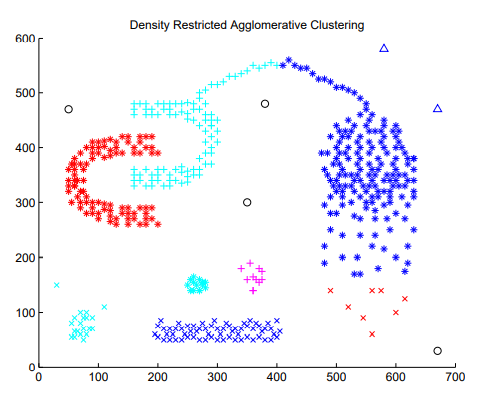
Fig 2: Clusters as discovered by DRAC

Image credits: Pattern Clustering using Cooperative Game theory

SHARPC cannot detect clusters that are not convex. If the threshold is increased to solve merging of different clusters (the light blue clusters in Fig 1), more clusters are formed and the larger clusters get subdivided into several small clusters.

The DRAC cluster (the light blue clusters in Fig 2) is highly dense; its cluster center has very high Shapley value. This results in a very high value of β, the similarity threshold. The red and light blue clusters are distinct. The red cluster is a low-density cluster (owing to the low Shapley value of the cluster center). It has a low β value, the similarity threshold, thus allowing more faraway points to be a part of the cluster.

References

[1] Wikipedia.org: Cluster Analysis

[2] eFinanceManagement: Cooperative Game Theory | Transferable utility, Example

[3] Swapnil Dhamal, et al.: Pattern Clustering using Cooperative Game theory

[4] Wikipedia.org: Cooperative Game Theory

[5] Wikipedia.org: Core (game theory)

[6] Wikipedia.org: Shapley value

Authored by: Kajol Sah, Consultant at Absolutdata